Vectors in Linear Algebra

Magnitude, Direction, Transpose, and Operations in Field.

What’s a vector

Simply put, a vector is a list of ordered numbers. Each element in a vector is also called a component or coordinate.

In the example below, a vector (x) is in the field of Real Numbers with n-dimensions.¹

\(\vec{x} \in \mathbb{R}^n\)

The vector has infinite elements, as denoted by the ellipsis.

\(\vec{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \end{pmatrix} \)

The following vector within a 2-dimensional field of Real Numbers has two elements.

\(\vec{x} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} \in \mathbb{R}^2\)

This essentially represents a line on a 2-dimensional plane.

The elements of a vector give instructions on how to get from the origin of a coordinate grid (e.g., x = 0, y = 0). In other words, where the tail of the vector begins, to its tip.

The first number is how far to move to the right or left along the x-axis, while the second is how far to move up or down the y-axis.

In the vector above, the first element, 4, represents the movement along an x-axis. The second element, 2, represents the movement along a y-axis.

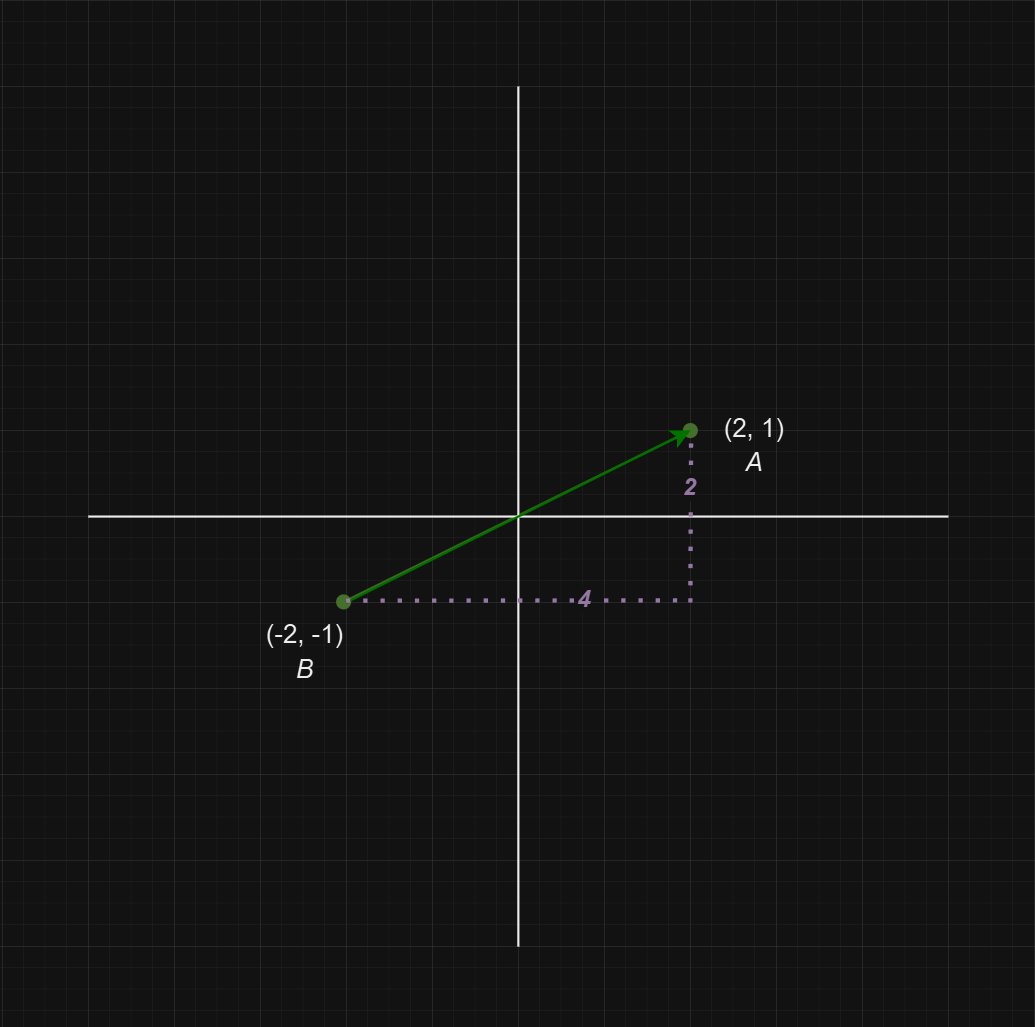
Visually, this could look like the following:

Starting from B, there are four movements to the right and then two movements vertically to reach A.

Mathematically, this would appear as:

\((-2, -1) + (2, 1) = \vec{x} = \begin{pmatrix} 4 \\ 2 \end{pmatrix}\)

Vector transpose

Vectors can be column vectors or row vectors. In Linear Algebra, a transpose is when a column vector takes the shape of a row vector or vice versa. The mathematical notation for a transpose is T.

\( \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\a_n\end{pmatrix}^T = \begin{pmatrix} a_1 & a_2 & \cdots\ a_n\end{pmatrix}\)

In other words:

\(\vec{x}^T = \vec{y}\)

Magnitude

Each vector holds a magnitude.

The symbol used for magnitude is || ||.

The Pythagorean Theorem calculates the magnitude of a 2D vector.

For example, take the vector:

\(\vec{x} = \begin{pmatrix} 4 \\ 2 \end{pmatrix}\)

The magnitude would be calculated as:

\(\| \vec{x} \|= \sqrt{4^2 + 2^2}\)

Where 4 is the horizontal element (e.g., four movements along the x-axis) and 2 is the vertical element (e.g., two movements along the y-axis).

Direction

Therefore, the angle created by moving along the two axes gives the direction of the vector. Looking at the vector visually, the angle is denoted by θ.

Trigonometry is used to calculate the angle:

\(\theta = \tan^{-1}\frac{y}{x}\)

Where y is the short side of the triangle and x is the long side.

In this case:

\(\theta = \tan^{-1}\frac{2}{4}= 26.56505^\circ\\)

---

Operations in the field

Vector addition

The mathematical definition of vector addition in the Real Numbers field is to add the elements entry by entry.

Take two vectors, for example:

\(\vec{x} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{pmatrix} \in \mathbb{R}^n\)

\(\vec{y} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_n \end{pmatrix} \in \mathbb{R}^n\)

The result of summing these two vectors will also be in the Real Numbers field.

\(\vec{x} + \vec{y} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \\ a_3 + b_3 \\ \vdots \\ a_n + b_n \end{pmatrix} \in \mathbb{R}^n\)

For example, take these two vectors:

\(\vec{x} = \begin{pmatrix} 5 \\ 2 \\ \end{pmatrix} \)

\(\vec{y} = \begin{pmatrix} -4 \\ -1 \\ \end{pmatrix} \)

The sum of the first element:

\(a_1 + b_1\)

is:

\(5+ -4 = 1\)

The sum of the second element:

\(a_2 + b_2\)

is:

\(2 + -1 = 1\)

Therefore:

\(\vec{x} + \vec{y} = \begin{pmatrix} 1 \\ 1 \\ \end{pmatrix} \)

Visually, this is the same as moving the tail of the second vector to sit at the tip of the first.

Then drawing a new vector from the origin of the first vector to the tip of the second vector.

The resulting third vector is said to be the sum of the original two.

Vector addition is the only time a vector will stray from the origin (x = 0, y = 0).

How does this look numerically?

In the example above, it is the same as:

• Five steps to the right (5)

• Two steps up (2)

• Four steps to the left (-4)

• One step down (-1)

Or :

• 5 + (-4) = 1

• 2 + (-1) = 1

Why is this a good definition of addition?

Think of each vector as a movement in space; a step with a distance and direction from some point of origin. Taking a step along the first vector and then a step along the second, the overall movement would be the same as the sum of the vectors, as described above.

It is the same as visualising movement on a one-dimensional number line. Taking two steps to the right and six further steps reaches position 8, just as if you were taking all eight steps simultaneously.

Scalar by vector multiplication

A scalar by vector multiplication is also defined by multiplying the vector elements entry by entry

If α∈R (that is, α is a number in the field of Real Numbers), and the vector is:

\(\vec{x} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{pmatrix} \in \mathbb{R}^n\)

Then, each vector element is multiplied by the scalar (α).

\(\vec{y} = \alpha\vec{x} = \begin{pmatrix} \alpha a_1 \\ \alpha a_2 \\ \alpha a_3 \\ \vdots \\ \alpha a_n \end{pmatrix} \in \mathbb{R}^n\)

Visually, scalar by vector multiplication extends the vector’s direction and increases or decreases the magnitude. Therefore, if the scalar is a fraction, the vector is reduced proportionally to that fraction.

Using a scalar of a negative number would flip the vector around to its opposite direction and then stretch it in that new direction.

Hence, the name “scalar” is used for scaling.

1. In mathematics, a field is a set equipped with two operations (typically called addition and multiplication) that satisfy certain properties, such as associativity, commutativity, distributivity, the existence of additive and multiplicative identities, and the existence of additive and multiplicative inverses for every element except the additive identity.

The field of Real Numbers, denoted by the “R,” represents the set of all real numbers. It is most commonly encountered in calculus, real analysis, and many applied fields.