Linear Combination

Span and Basis Vectors, and linear (in)dependence.

The “simple” definition of a linear combination is multiplying a scalar by a variable and adding those terms.

If x, y, and z are variables, and a1​, a2, and a3 are scalars, then the following equation will be a linear combination.

\(v = a_1 x + a_2 y + a_3 z\)

If the variables are vectors, then the linear combination of a scalar by a vector will be a new vector:

\(\vec{v} = a_1 \vec{x} + a_2 \vec{y} + a_3 \vec{z}\)

The general notation of a vector by a scalar linear combination will be:

\( \sum\frac{n}{1}\ a_i \vec{v}_i \)

What is Span

The span of a set of vectors is the set of all possible linear combinations of those vectors.

Mathematically, the span of the set of vectors is written as:

\(Sp(\vec{v}_1,\vec{v}_2,...\vec{v}_n)\)

This represents all possible vectors that can be formed by taking linear combinations of the vectors with real scalars.

In the case of two vectors in 2-dimensional space, if the vectors are not linearly dependent (i.e., they do not lie on the same line), their span will be the entire 2-dimensional space, meaning they can reach any point in that space. However, if the vectors are linearly dependent (i.e., they lie on the same line), their span is limited to all vectors along that line.

For example, the following three vectors would span the entire R3 space (the 3-dimensional vector space over the field of real numbers) because they are linearly independent. This means that no vector in the set can be expressed as a linear combination of the others, and together, they can represent any vector in R3

\(\vec{v}_1 = \begin{pmatrix}1 \\0 \\0\end{pmatrix}, \vec{v}_2 = \begin{pmatrix}0 \\1 \\0\end{pmatrix}, \vec{v}_3 = \begin{pmatrix}0 \\0 \\1\end{pmatrix}\)

Span and 3-dimensional space

The concept of span is more interesting in 3D space. Take two vectors that are not pointing in the same direction. What does it mean to take their span?

In this case, the span of the two vectors is the set of all possible linear combinations of these vectors. Geometrically, this means that the span of these two vectors forms a plane in 3D space. Every vector (or point¹) on this plane can be represented as a linear combination of the two original vectors.

Now, consider three vectors that are not all lying in the same plane. What happens when you take their span?

A linear combination of three vectors is essentially the same as it is in 2-dimensional space:

\(a \vec{v} + b \vec{w} + c\vec{u}\)

In 3D space, the span of three linearly independent vectors (that do not lie in the same plane) is the entire 3-dimensional space. This means that any vector/point in the space can be expressed as a linear combination of the three vectors.

So, the span of the vectors v, w, and u is the set of all possible vectors you can create by varying the scalars a, b, and c in the linear combination above. When these three vectors are linearly independent, their span covers all of 3D space.

Linear dependence

When a set of vectors is said to be linearly dependent, it means that at least one of the vectors in the set can be expressed as a linear combination of the others. In other words, some vectors in the set are redundant because they do not add any new direction (or span) to the vector space that the other vectors already cover.

Linearly dependent vectors do not contribute to increasing the span of the vector space.

In n-dimensional space, if a set of vectors is linearly dependent, the span of these vectors does not cover any additional directions beyond what is already covered by a subset of these vectors. Consequently, the set does not form a basis for the vector space, as a basis requires all vectors to be linearly independent, ensuring that they span the entire space without redundancy.

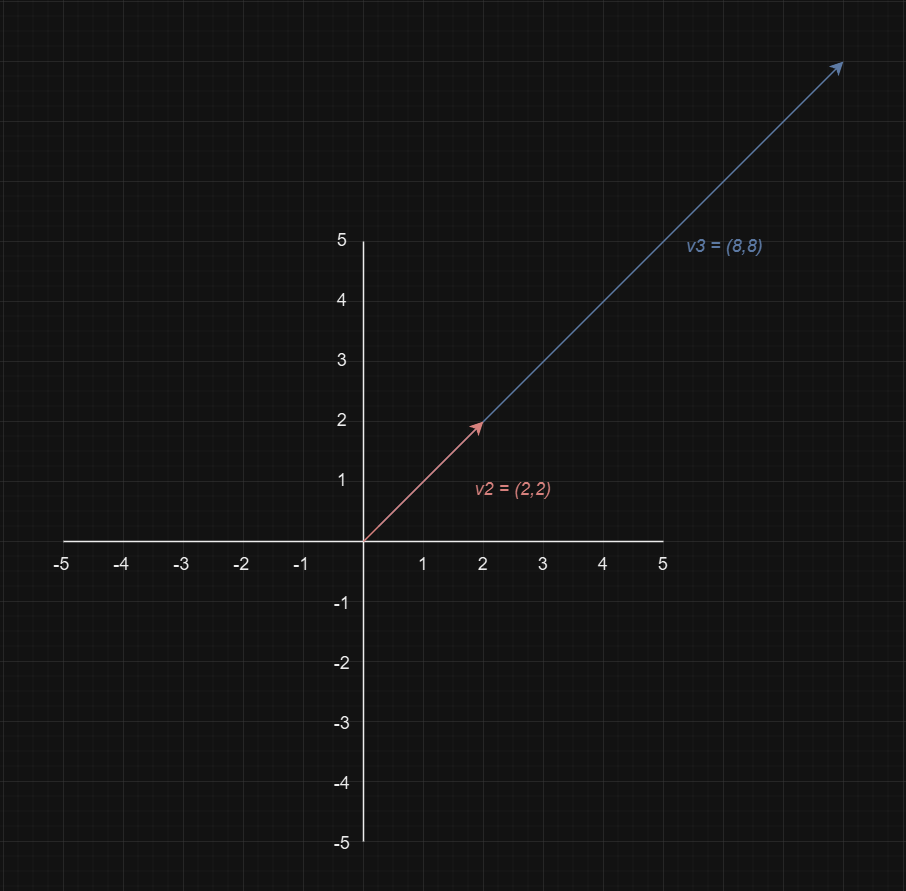
For example, take the following two vectors:

\(\vec{v}_2 = \begin{pmatrix}2 \\2 \\2\end{pmatrix}\)

and:

\( \vec{v}_3 = \begin{pmatrix}8 \\8 \\8\end{pmatrix}\)

These represent a linearly dependent set. Notice that each component of v2 is precisely one-fourth of the corresponding elements of v3.

Specifically:

\(\vec{v}_3 = 4 \times \vec{v}_2\)

This means v3 is simply a scaled version of v2. They are not independent because v3 can be written as a scalar multiple of v2. In other words, v2 and v3 lie along the same line in 3D space but at different magnitudes.

Visualising this concept in 3-dimensional space can be challenging. Consider a graphical representation with just two components in each vector for simplicity. As shown, the span of one vector is entirely encompassed by the other.

3Blue1Brown has great visualisations in his videos that better demonstrate exactly how this limits access to further span in a 3-dimensional vector space.

Linear independence

When each vector in a set of vectors can not be defined as a linear combination of the other vectors, they are said to be linearly independent.

That is, for all values of a:

\(\vec{w} \neq a\vec{v}\)

Or for all values of a and b:

\(\vec{u} \neq a\vec{v} + b\vec{w}\)

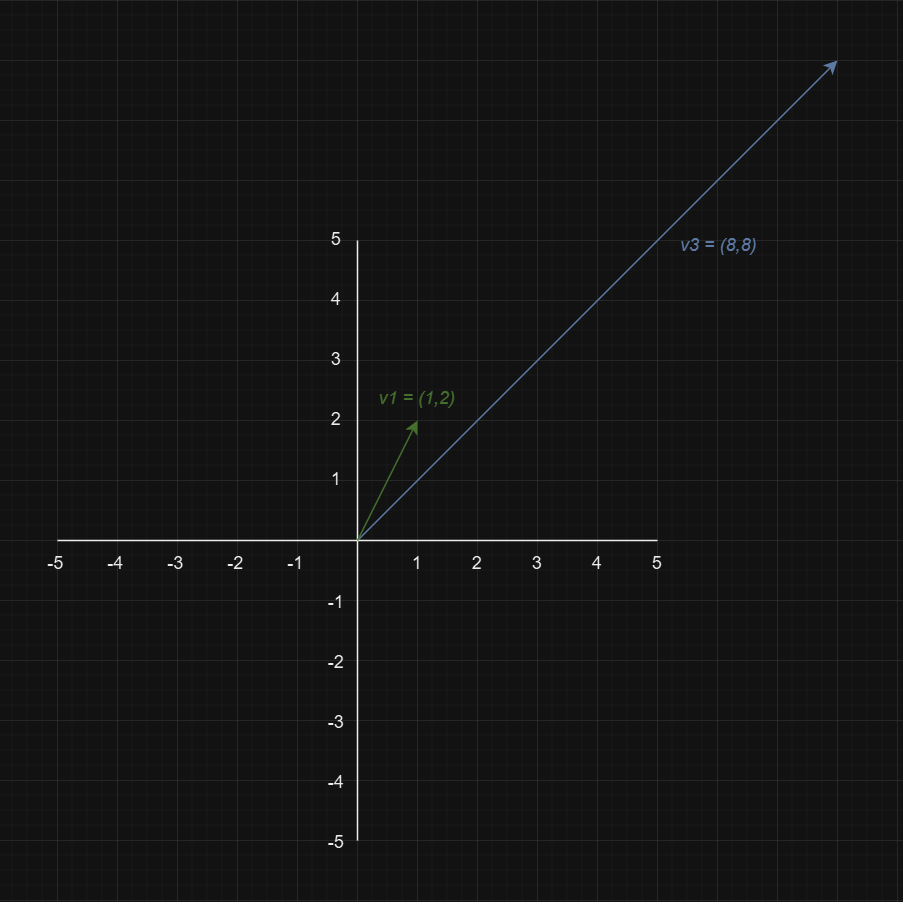
For example:

\( \vec{v}_1 = \begin{pmatrix}1 \\2 \\3\end{pmatrix} ,\ \vec{v}_3 = \begin{pmatrix}8 \\8 \\8\end{pmatrix}\)

These vectors are linearly independent.

To check if the vectors are linearly independent, there should be no scalar, k, such that:

\(v 3 ​ ​ \neq k⋅ v 1 ​ ​ \)

In other words, each component of v3 can not be equal to the corresponding components v1 multiplied by k.

For:

\(\vec{v}_1 = \begin{pmatrix}1 \\2 \\3\end{pmatrix} ,\ \vec{v}_3 = \begin{pmatrix}8 \\8 \\8\end{pmatrix}\)

This would require:

\(k⋅1=8 ,\ k⋅2=8 ,\ k⋅3=8\)

To solve for k in the components:

\(\begin{array}{c} \text{From the first component:} \quad k = \frac{8}{1} = 8 \\ \text{From the second component:} \quad k = \frac{8}{2} = 4 \\ \text{From the third component:} \quad k = \frac{8}{3} \approx 2.67 \end{array}\)

The vectors are linearly independent since no single scalar k satisfies the equation for all components.

Again, this is challenging to represent on a 3-dimensional plane (see the video above!), but taking the first two components illustrates linearly independent vectors.

A note on basis vectors

The technical definition of a basis of a vector space is a set of linearly independent vectors that span the full space.

• Linearly Independent: No vector in the set can be written as a linear combination of the others. This ensures that all vectors in the basis contribute uniquely to spanning the space.

• Span: The set of vectors can be combined (through linear combinations) to form every possible vector in the space.

If you have a basis for a vector space, you can represent any vector in that space as a unique linear combination of the basis vectors.

î and ĵ are the “basis vectors” of the xy coordinate system.

\(\hat{\imath} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \hat{\jmath} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}\)

In the xy coordinate system,

• î represents the unit vector in the direction of the x-axis.

• ĵ represents the unit vector in the direction of the y-axis

By taking linear combinations of these basis vectors, every possible 2-dimensional vector can be expressed.

Whenever vectors are described numerically, it implicitly assumes a choice of basis vectors, typically î and ĵ in 2-dimensional Cartesian coordinates. Changing the basis vectors changes the representation of all vectors in that space, though the vectors themselves remain unchanged.

A system of Linear Equations

A linear combination of vectors by scalars is crucial in solving systems of linear equations. For instance, suppose a vector needs to be represented as a linear combination of two other vectors.

Consider the following vector:

\( \vec{v}= \begin{pmatrix}-13 \\2\end{pmatrix}\)

Which needs to be the linear combination of:

\(\vec{x}= \begin{pmatrix}-14 \\2\end{pmatrix}, \quad \vec{y} = \begin{pmatrix} 5 \\ -1 \end{pmatrix}\)

In this situation, the equation solves for scalars a and b, where a and b represent the coefficients of x and y, respectively:

\(a\vec{x} + b\vec {y} = \vec{v}\)

First, multiply each vector by its corresponding scalar:

\( a \begin{pmatrix}-14 \\2\end{pmatrix} + b \begin{pmatrix}5 \\-1\end{pmatrix} = \begin{pmatrix}-13 \\2\end{pmatrix}\)

Which is:

\( \begin{pmatrix}(-14)a \\2a\end{pmatrix} + \begin{pmatrix}5b \\(-1)b\end{pmatrix} = \begin{pmatrix}-13 \\2\end{pmatrix}\)

The above results gives two separate equations:

\(\begin{cases} \begin{aligned} -14a + 5b &= -13 \\ 2a - b &= 2 \end{aligned} \end{cases}\)

These equations form a system of two equations with two unknowns.

There are three theoretical methods to solve the equations.

Substitution Method

To solve a system of equations by substitution, first, isolate a variable from one of the equations and substitute it into the other. This reduces the system of equations to a single equation with a single unknown.

Equation 1

\(-14a + 5b = -13\)

Equation 2

\(2a - b = 2\)

Step 1 - Solve one equation for one variable

Starting with Equation 2 for b in terms of a:

\(2a - b = 2\)

To isolate b, add b to both sides and subtract 2 from both sides:

\(b = 2a - 2\)

Now b is expressed in terms of a.

Step 2 - Substitute the expression into the other equation

Substitute the expression for b from Equation 2 into Equation 1:

So Equation 1 goes from:

\(-14a + 5b = -13\)

to:

\(-14a + 5(2a - 2) = -13\)

Step 3 - Simplify and solve for a

Expand the equation:

\(-14a + 10a - 10 = -13\)

Combine like terms:

\(-4a - 10 = -13\)

Isolate the term with a by adding 10 to both sides:

\(-4a - 10 +10 = -13 + 10\)

becomes:

\(-4a = -3\)

Divide both sides by -4 to solve for a:

\(a = \frac{-3}{-4} = 0.75\)

Step 4 - Substitute back to find b

Now that a = 0.75, substitute this value back into the expression for b:

\(b = 2a -2\)

Substitute a = 0.75:

\(b = 2(0.75) - 2\)

Which equals:

\(b= 1.5 - 2\)

which is:

\(b= -0.5\)

Step 5 - Verify the solution

To ensure the solution is correct, substitute a = -0.75 and b = -0.5 back into the original equations.

Check Equation 1

\(-14a + 5b = -13\)

Substitute a for 0.75 and b for -0.5:

\(-14(0.75) + 5(-0.5)\)

this equates to :

\( -10.5 - 2.5 = -13\)

Check Equation 2

\(2a - b = 2\)

Substitute a for 0.75 and b for -0.5:

\(2(0.75) - (-0.5)\)

and equates to:

\(1.5+0.5=2\)

Final answer:

The solution to the system of equations is:

\(a = 0.75 ,\ b = -0.5\)

This solution satisfies both equations, confirming the calculations are correct.

Elimination Method

In this method, one of the variables is eliminated by enforcing the same absolute value for one of the coefficients (scalars) in the two equations.

The equations again are:

\(\begin{cases} \begin{aligned} -14a + 5b &= -13 \\ 2a - b &= 2 \end{aligned} \end{cases}\)

If Equation 2 is multiplied by 5, the equations become:

\(\begin{cases} \begin{aligned} -14a + 5b &= -13 \\ (2*5)a - 5b &= 2*5 \end{aligned} \end{cases}\)

simplified to:

\(\begin{cases} \begin{aligned} -14a + 5b &= -13 \\ 10a - 5b &= 10 \end{aligned} \end{cases}\)

Step 1: Add the Equations

Now, add the two equations to eliminate b and obtain a single equation with a single unknown:

\((-14a + 5b) + (10a - 5b) = -13 + 10\)

This becomes:

\(14a+10a=−3\)

Combine like terms:

\(-4a = -3\)

Step 2: Solve for a

To solve for a, isolate a by dividing both sides by -4:

\( \frac{-3}{-4} = \frac{3}{-4}\)

\(a = \frac{3}{4}\)

Or:

\(a = 0.75\)

Step 3: Substitute back to Find b

Now that a = 0.75, substitute this value back into the expression for b:

\(2a - b = 2\)

Substitute a = 0.75:

\(2(0.75) - b = 2\)

Which equals:

\(1.5 - b = 2\)

Subtract 1.5 from both sides:

\(-b = 0.5\)

Multiply both sides by -1:²

\(b = -0.5\)

Final answer

This means scalars a = 0.75 and b = -0.5 represent the vector:

\( \vec{v} = \begin{pmatrix}-13 \\2\end{pmatrix}\)

as a linear combination of vectors x and y.

Substituting the vectors

\( \begin{pmatrix}-13 \\2\end{pmatrix} = a\ \cdot \begin{pmatrix}-14 \\2\end{pmatrix} + b \cdot \begin{pmatrix}5 \\-1\end{pmatrix}\)

is:

\(\begin{pmatrix}-13\\2\end{pmatrix} = 0.75 \cdot \begin{pmatrix}-14 \\2\end{pmatrix} + (-0.5) \cdot\begin{pmatrix}5 \\-1\end{pmatrix}\)

is

\( \begin{pmatrix}-13 \\2\end{pmatrix} = \begin{pmatrix}-10.5\\1.5\end{pmatrix} + \begin{pmatrix}-2.5 \\0.5\end{pmatrix}\)

Graphical Method

When using the graphical method to solve a system of linear equations by drawing the lines on a plane, calculate the following:

Step 1: Slope-Intercept Form of Each Equation:

The general form of a linear equation is y = mx + c, where:

• m is the slope of the line.

• c is the y-intercept (when x = 0).

For each equation, rearrange it into the slope-intercept form y = mx + c.

Given the system of equations:

\(\begin{cases} \begin{aligned} -14a + 5b &= -13 \\ 2a - b &= 2 \end{aligned} \end{cases}\)

Equation1:

\(−14a+5b=−13\)

To solve for b, isolate b on one side:

\(5b=14a−13\)

Now, divide by 5 to solve for b:

\(b = \frac{14}{5}a - \frac{13}{5}\)

This is the slope-intercept form of the equation in terms of y = mx +c.

Equation 2:

\(2a - b = 2\)

To solve for b, isolate b on one side:

\(- b = -2a + 2\)

Now multiply the entire equation by -1 to solve for b:

\(b=2a−2\)

This is the slope-intercept form of the equation in terms of y = mx +c.

Step 2: Plot the Lines:

Equation 1
Start by plotting the y-intercept at:

\((0, \frac{13}{5})\)

Use the slope to find another point. For every five units moved to the right, increase b by 13 units.

Equation 2

Start by plotting the y-intercept at:

\((0,2)\)

Use the slope 2 to find another point. For each 1 unit moved to the right, b increases by two units.

Step 4: Find the Intersection Point:

The point where the two lines intersect is the solution of the system of equations.

This point corresponds to the values of x and y that satisfy both equations simultaneously.

In this case the point of intersection (the solution to the system of equations) is:

\((\frac{3}{4}, -\frac{1}{2})\)

or:

• a = 0.75

• b = -0.5

Vectors vs. Points

1. When thinking about individual vectors, conceptualise them as arrows. When dealing with a collection of vectors, it is easier to think of them as points in an n-dimensional vector space.

2. The goal is to solve for b. To do this, you need to isolate b. Since the equation has −b (negative b), multiplying both sides of the equation by −1 will make b positive.